Princess Mereret lived during the 12th Dynasty reign of her father Senusret III (1878-1839 BC). This open pectoral was found in her tomb in the funerary complex of Senusret III in 1894 and can be seen in the Cairo Antiquity Museum. It's a cloisonne with a framework of gold, and cells inlaid with pieces of carnelian, lapis lazuli, turquoise and amethyst with polychrome glaze. Does it have a geometric feel to it? It should, because it's been very carefully designed by a consistent geometric scheme guiding and integrating each element with each other and to the whole. Everything has a mirror reflection to it, symbolizing our world of polarity, except one element (do you see it?) which doesn't belong to the mortal realm. The overall scene is of a "chapel", a sacred space, between growing lotus columns at the sides. At top is the virgin vulture goddess Nekhbet with outstretched wings protecting the griffins, mythical creatures which combine the powers of the falcon with the strength of the lion, both solar symbols. They wear the double-feather crown and so represent the pharaoh, who smites Libyans with his fists and legs, and tramples on Nubians below him. Between the two griffins is a cartouche containing the throne name of the pharaoh, Kha-khau-re, meaning "Appearing like the Souls of Re". This scene on the pectoral is usually interpreted historically as representing battles Senusret III engaged in, but is also a spiritual teaching about overcoming hindering elements within ourselves and transforming inner chaos to order.
The hidden geometric framework with which it was designed isn't overtly evident. Yet it yields its secrets if we begin (below) by overlaying a circle with an inscribed hexagon over the scene. (This construction upon this pectoral and another of Mereret's can be done in Constructing The Universe Activity Book Volume 2, page 126.) A hexagram star is drawn between the six points so that the bottom of the upward pointing triangle matches the bottom of the pectoral. We immediately notice that the lotuses lean inward, and the small uppermost triangle frames the vulture's torso. In fact, the circle at the base of her neck (the only element with no reflected symmetry) is at the exact center of this small triangle (red lines). In Egyptian art, an upward pointing triangle is considered a place of great honor. The two sides of this large upward-pointing triangle also skim along the edges of the feathered crowns, continuing downward precisely between their horizontal horns and the lotuses and tails. We also notice the large rectangle (yellow top and bottom, with black sides) which contains most of the scene. This is a square-root-of-three rectangle found in every regular hexagon, which Egyptian mathematics was familiar with and used in the designs of scenes and proportions of objects considered sacred, sharing the symbolism of the auspicious number three.

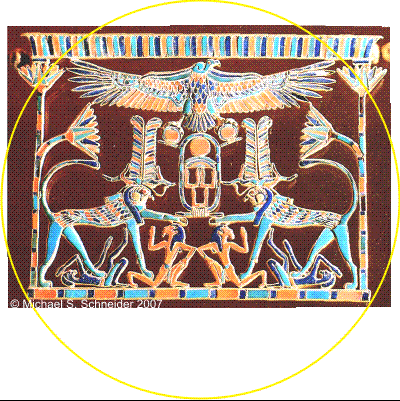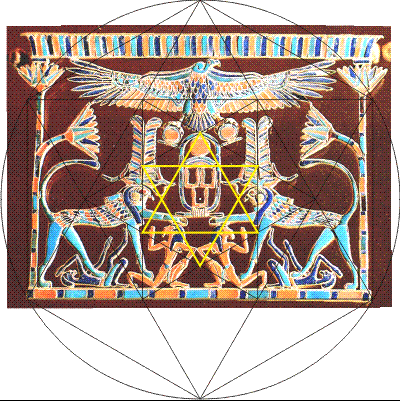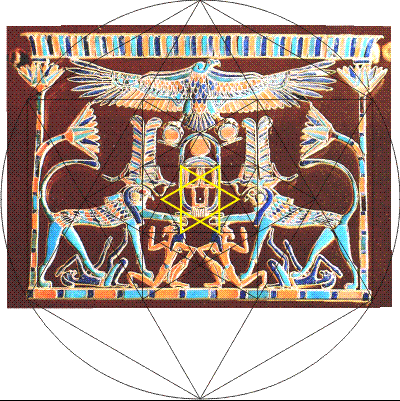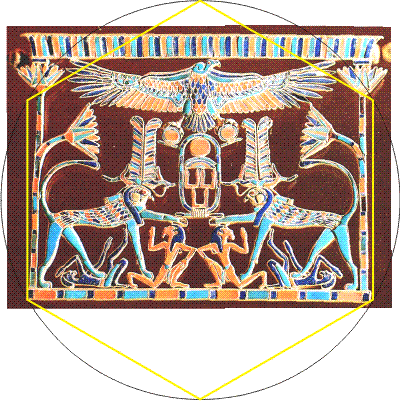
The method for seeing the geometric framework of this composition is simply to draw smaller hexagram stars within central hexagons. Here, a smaller, turned (yellow) hexagram is drawn in the hexagon made by the crossings of the larger hexagram. Lo and behold! Its two vertical lines go precisely down through the center of each double-feather crown. In doing so, they divide the large root-three rectangle into three equal parts. What is remarkable is that each of these parts is a smaller, turned root-three rectangle which models the whole. Notice how the vulture's tail feathers nestle in the upper central crossing which defines the top of the central cartouche, and the shen ring ("eternity") glyphs in her claws find their place. Below, the lines limit the length of the Libyans' hair and bent knees. And below right, a red square drawn in the top of the central root-three rectangle clearly defines the placement of the griffins' paws supporting the cartouche. Two green root-three rectangles below the square frame the paws (and Libyans), as well as the width of the rope-binding at the bottom of the cartouche.


The next smaller hexagram divides the central vertical root-three rectangle into three smaller horizontal root-three rectangles, creating guidelines for various elements. It was a common technique, when depicting gods and goddesses, to place them precisely on and along the lines. This conveys an eternal feeling, as the geometry is eternal. But mortal creatures, including the pharaoh and his enemies on the field of transitory life are placed not upon the lines but alongside them, and at slight angles to them, which gives a feeling of movement and so is appropriate for scenes from the realm of life.

By the way, if you've been wondering why the hexagonal geometry doesn't seem to account for the full height of the pectoral, while its width at the base equals the bottom of the large root-three rectangle, here's why: the Egyptians determined the height from points within the central construction. In this case, the length (red lines) between the bottom corners of the pectoral and a corner of the hexagram star we just drew. To determine this pectoral's height, simply place a compass point at the bottom corner of the pectoral (the bottom of one red line) and open the pencil to its other end (at one corner of the yellow triangle). Swing the compass upward (along the white arrows) until they cross the upward extensions of the sides of the root-three rectangle. (Math: If the short side of the smallest yellow root-three rectangle equals 1 unit, then the red radius simply equals 4.) Simply put, the white rectangle at top equals three root-three rectangles side by side. So the whole pectoral may be thought of as twelve (=3x4) of these root-three rectangular areas. Other pectorals use these and other points within nested polygons, rectangles and other constructions to determine any extending elements. Using proportions found within the construction maintains design unity.


Another, smaller hexagram drawn within the previous one reveals the width of the central cartouche, which nestles in the hexagram's crossings above each griffin's upper paws.

Another, even smaller hexagram encloses the glyph of arms and hands upright in praise, the ka glyph, symbol of the sacred soul. (Three kas of the name in the cartouche indicates the plural, or "souls" of Re.) The bottom of the upward triangle frames the bottom of the cartouche's oval.

The vertical lines of this sixth, smallest and final hexagram perfectly match the upright arms of the ka glyph. Between them is the central point of the construction, of all the nested hexagrams, which is an important point of interest of the scene. What this says symbolically is that the whole construction grows in an orderly fashion from this seed by the praise of one's ka. Unified order occurs because each smaller root-three rectangle continuously divides into three smaller, identical replicas, which modern mathematicians might call fractals. Thus, every element of the geometry, and of the scene, maintains a unity of ratio throughout the diversity of sizes. It creates the feeling of a coherent, harmonious whole. The Egyptians were masters of this, and the technique is found in worldwide art, crafts, architecture and design to this day.

Since you've come all this way, here's something different for your appreciation: an animation of the developing stages of this geometric construction for you to feel its breathing, its rhythm of growth and dissolution, and so to understand it somewhat as the Egyptians did. They valued mathematical order in their sacred art as they observed it in nature. Perhaps you can replicate the construction with a compass and straightedge, and design something important to yourself in it.