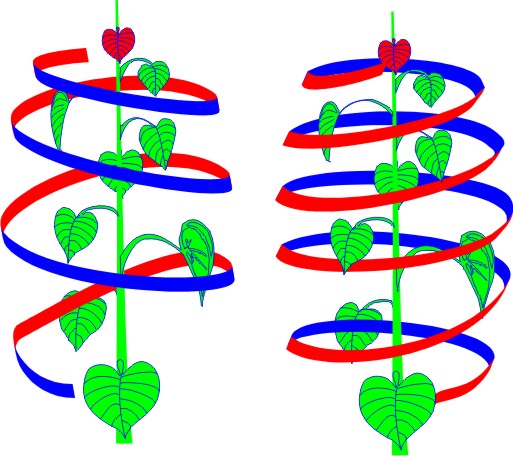
5 turns in the other, resulting in 8 leaves3 turns complete a cycle in one direction 5 turns in the other, resulting in 8 leaves
Our modern word "cosmos" refers to outer space, the universe, a wild place where nearly anything can happen among exploding stars, clashing galaxies and black holes swallowing it all. In my opinion, this isn't the basis of a constructive world view. A more psychologically healthy worldview comes from ancient Greece, where the word kosmos meant an "adornment" like embroidery, implying a universe of orderly, rhythmic patterns and harmony among its parts. A convenient way to see these orderly patterns, rhythmns, and harmonious relationships on Earth is by observing the ubiquitous plant world. Its patterns are mathematical and are easy to see, and can help to build up a feeling of order and harmony in yourself.
I enjoy seeing mathematical ideas made visible, and with geometric models we can admire the plant world's own beautiful mathematical harmonies.
Nothing has to be done to an actual plant to make it's mathematics visible, although with their complexities, it may be difficult to see. So I made models of very simplified versions of idealized plants. Botanists use the word "phyllotaxis" to refer to the arrangement of leaves on a stem, or branches on a trunk.
The important mathematical idea here concerns the Fibonacci Numbers, a sequence which builds upon its immediate past, just as plants do: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, .... Naturally, each two terms add to make the next.
Each of these models is built upon two opposite-spinning spirals, having consecutive Fibonacci numbers as their number of turns. Where these opposing spirals cross, approximately 137.5 degrees apart, a leaf, branch, flower or fruit appears. This gives each leaf the most space, maximum exposure to sunlight and rain, and provides the best weight distribution for the plant's overall balance.
Notice how in each of these models, when seen from above, the "sun's-eye-view," we can see most of the flowers at once.
Yellow Roses
5 turns of the white spiral
8 turns of the red spiral
13 yellow flowers where the spirals cross
The yellow flowers form 2 spirals upward in one direction, 3 spirals in the other.
Blue Roses
1 plant
2 opposing spirals
3 columns of flowers spiraling up in one direction
5 columns of flowers spiraling in up the opposite direction
8 turns of the silver spiral
13 turns of the green spiral
21 blue flowers where the spirals cross
Red Roses and Moss
8 turns of an unseen spiral
13 turns of the silver spiral
21 red flowers where the spirals would cross
21 green moss clumps between the roses
Resting Butterflies
In place of flowers, butterflies alight in this maximized pattern.
3 turns of the silver spiral
5 turns of the purple spiral
8 butterflies where the spirals cross
Perching Birds
8 turns of the silver spiral
13 turns of an unseen spiral
21 birds where the spirals cross
© Michael S. Schneider 2018