When scholarship in Europe declined during the Dark Ages, priceless Hellenistic and other works of antiquity, including mathematics, were virtually lost to them, surviving only in the Christian Monastaries. When the Muslim Arabs conquered parts of Asia, Europe, and North Africa in the late 7th and early 8th centuries they'd developed few artistic traditions of their own, and only the simplest mathematics. But through their conquests they absorbed and modified elements of Byzantine, Coptic, and Persian art and mathematics, which took root in Islamic centers of learning and developed various ways.

When India's second Mughal emperor, Humayun (reigned 1530-1540 and 1555-1556) was visiting Tabriz, Persia, in the Safavid court of Shah Tahmasp I, he was exposed to Persian miniature painting. Greatly impressed, he returned to India with two accomplished Persian artists, Sayyid Ali and Abdus Samad. Their works were assimilated with local styles, and during succeeding decades gave shape to a distinct style known as Mughal painting.

When Nadir Shah of Persia invaded the Indian plains in 1739, Hindu artists trained as Mughal miniature painters fled north to the Kangra Valley of the Himalayan foothills (I visited there in 1977, staying on Dal Lake and elsewhere). There, influenced by the landscape, they developed a style of painting using the colors of the dawn and the rainbow, pure colours of earth and minerals and emphasizing cool blues and greens, yellows and warm reds. These "Kangra style" paintings often portray a spirituality of feeling marked by liquid grace and delicacy. The Kangra style reached its peak during the reign of Sansar Chand II (1775-1825), a great patron of the arts, and it continued to the end of the 19th century.

Kangra paintings often come in related sets. This painting (above), known as "Kurma the Tortoise" is from a set of Kangra Paintings of the Bihari Sat Sa which are based on a beautiful set of poems from Hindu mythology about the incarnations of the god Vishnu. It's found today in the National Museum of India in New Delhi. This painting depicts a tale of the eleventh incarnation of Vishnu where he took the form of a tortoise whose shell served as a pivot for the Mandaracala Hill, which was being used as a churning rod by the Devas ("angels") and Asuras ("demons") of the universe. Their back-and-forth tugging churned the sea to produce soma, the amabrosial sacred nectar which they could drink and become deathless.

Observers of these paintings often comment that their lines, forms and colors combine to produce a rhythmical and harmonious musical effect. This is no accident. These paintings are composed by a combination of science, art and religion. At their heart is a knowledge of aesthetic geometry deriving from the ancient world. When I first saw this painting I wondered not only at its overall proportions but of the two painted rectangles, green and blue, of the background. Having studied the proportions of a great many examples of art, it's clear that the sacred art of every sacred tradition was undoubtedly and intentionally designed with mathematical and symbolic considerations. Mathematics was considered a sacred language, not invented by anyone but it can be discovered, eternally true. Spiritual artists saw its significance and value, and used carefully considered mathematics to express sacred arts, crafts, architecture, dance, poetry, literature and more. I became curious about the proportions they selected for these rectangles, and so I looked into these and other Kangra paintings.

Before even examining them, the first hints I noticed were the paintings' origins in mythology and poetry, and constant references to its musical feel. In ancient India, sacred literature and poetry was always composed, down to the level of the syllable, with particular mathematical rhythms which produce certain feelings. And their musical scales are well-documented to have a mathematical basis. So it was no surprise to find that the overall painting (within the frame) is a two-by-three rectangle. Two-by-three, or two-thirds, is an obvious musical ratio. Plucking two-thirds of a vibrating string will always produce a note five steps higher than the sound made by plucking the full string. This is the musical interval known as the "perfect fifth", also known as the "chord of truimph" for its exuberant feel. Below (left) is a two-by-three rectangle. Notice how it is also the ratio around the two intersecting circles of the Hindu Mandorla ("almond", known in the West as the Vesica Piscis, "bladder of the fish"). It is a symbol of the polarity of creation and is the basis of geometric construction. Thus, it's symbolically appropriate for the theme of this painting, the back-and-forth churning of the cosmic ocean to create ambosia. Below (right) we see the two-by-three grid overlaid upon the painting. Notice how the top of Vishnu's crown is two-thirds of the way up the painting, at the top of the lower circle, reinforcing the musical "perfect fifth". The lowest part of the upper circle shows the rope as a chord of the circle.

But what about the inner green and blue rectangles representing the land and ocean? Their interface isn't clearly indicated by the two-by-three grid or its simple divisions. But the marvel of these designs is found in the ways that this simple, rational, two-by-three grid is further subdivided. The secret here is to extend the top two squares to become two Golden Rectangles. Below, left, we see the simple development of the square into Golden Rectangle. A red "diagonal" from the middle of the left side to an opposite corner swings an arc downward, giving us the yellow rectangle, a Golden Rectangle. The whole is also a Golden Rectangle. The second illustration shows this construction applied to both squares at the top of the two-by-three grid. Now we clearly see that the painting's top green area is framed as two side-by-side Golden Rectangles. The narrow horizontal rectangle below each yellow rectangle, but above the lowest squares, is equal to two small squares plus a smaller Golden Rectangle, or a square plus horizontal Golden Rectangle. (Thus it's also known as a "Phi-squared" rectangle, since Phi squared equals Phi plus one, with a ratio of 2.618... to 1) This is the wonder of Golden Mean mathematics: it always derives from, and reproduces, itself. It is self-referential and symbolic of unity in diversity. The third illustration overlays this geometry onto the painting. In the final illustration below (right) we see the remaining rectangle framing the blue ocean. This scheme is the essential geometric armature on which a number of paintings in this series were composed, although with clever and beautiful variations. From here we can look further into its geometric composition.

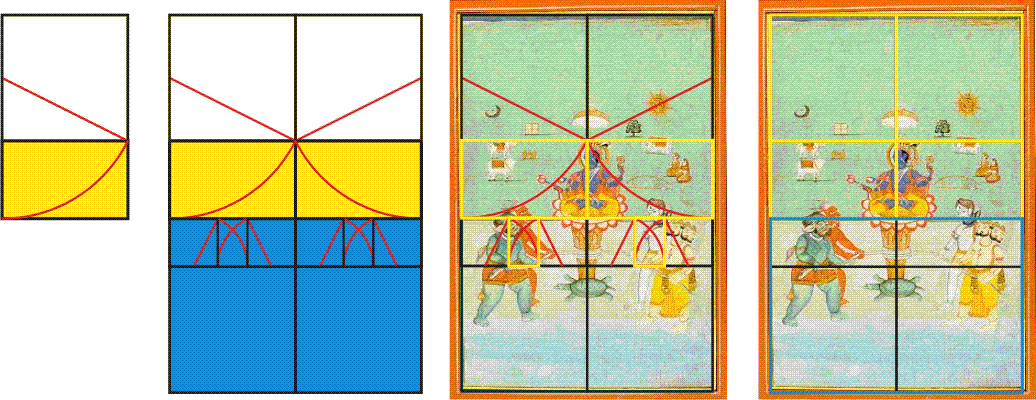
How can we reform this lower blue rectangle so that it gives us a structure to understand the lower composition? We identified it as two squares topped by two Phi-squared rectangles. But to see more we must reformulate this space into a square plus a Root-Five rectangle (a retangle whose sides are in square-root-of-five to one ratio, or 2.236... to 1. The whole blue rectangle is thus also known as a 1.447... rectangle.) Below, left, we see the construction of a Root-Five rectangle within a square. At right we see the root-five rectangle next to the square, filling out the painting's bottom rectangle.

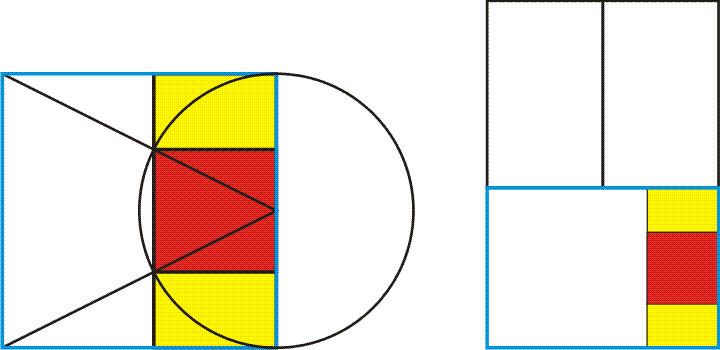
Next, we mirror the Root-Five rectangle on the other side of this lower rectangle, and begin to divide Golden Rectangles into squares (red) and smaller Golden Rectangles (yellow). In the picture below, right, we see this scheme overlaid upon the painting. More of the structure of its elements are seen to align with the geometry. Notice how the tortoise rests upon a symbolic square foundation, and Vishnu sits upon a lotus within two small Golden Rectangles, a miniature replica of the whole top geometry. The Asuras and Devas are held apart within a mirror-symmetry of Root-Five rectangles.

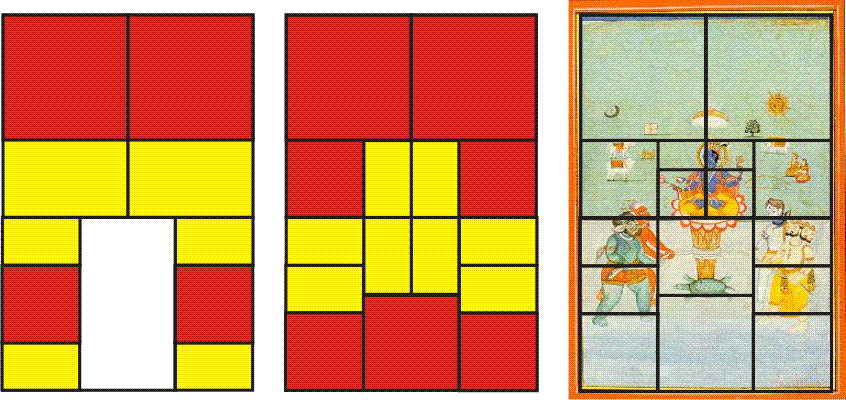
It's always geometrically possible to divide any Golden Rectangle or square into smaller Golden Rectangles and squares. But it's impossible to know the degree of geometric detail to which the designer of this painting took it. One analysis (below) seems to indicate that each of the central elements of the tortoise, shaft, rope, lotus and Vishnu was carefully proportioned to maintain the coherent balance provided by Golden Mean geometry. It's possible to find the placement of further elements through the geometry of simple lines and areas. Perhaps you can discover them.

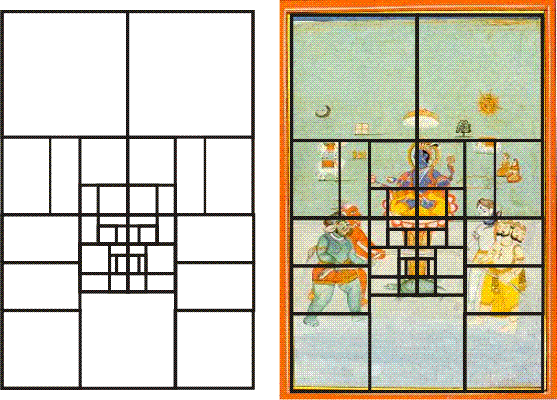
Other paintings in this series were similarly composed. Below are two more examples. Left, we see Vishnu in his incarnation as the fish Matsya saving a devotee. The geometry is essentially identical with that of the previous painting, with two Golden Rectangles over another rectangle. In the second painting (below, right) we see Vishnu in his 19th incarnation as Krishna playing the flute for his love Sita. It, too, is framed in a musical two-by-three rectangle grid. Notice how its very simplest diagonals emphasize their hearing: the blue diagonal joins Krishna's and Sita's ears, while the yellow and red diagonals cross the blue line precisely at each of their ears. In fact, Krishna's ear is at the exact center of the entire painting. If this is a coincidence then it's a quite marvelous set of them! But I'm sure it wasn't accidental, instead revealing how its designer was trained and thought. Today, many artists and art teachers disdain the use of mathematics is art, thinking that such rationality will destroy the subtle feeling of a work. But these paintings, and the wisdom and greatness of ancient sacred art in general, show that narrow thinking to be faulty when in the hands of educated experts. Perhaps you'll be inspired by these examples to explore other paintings in this series, or Kangra art in general, where simple but elegant geometric principles apply. Or perhaps you'll use this harmonious musical geometry to design something important to you.

More activities involving art and Golden Rectangle grids may be found in Constructing The Universe Activity Book Volume 3