Geometry of a
Herter Brothers Cabinet
by
Michael S. Schneider
M.Ed. Mathematics
Metropolitan
Museum Of Art, New York
Cabinet for Oliver Ames, Boston, c1883
Gift, in honor of the 75th Anniversary
of The American Wing, 1999 (1999.79), from
Robert L. and Ann R. Fromer, and Margot Johnson Inc.
During the late nineteenth century (1864 to
1906), Herter Brothers, the New York firm of the German-born brothers
Gustave and Christian Herter, was arguably the leading cabinetmaking
and decorating firm in the United States. Their work was in great
demand by the most affluent clients of this opulent era. This
rare cabinet, made for Oliver Ames of Boston, an industrialist
and governor of Massachusetts from 1886 to1888, is made of painted
and gilded maple wood, glass, brass and silk velvet.
Herter Brothers furniture
is one of the many places I look to in order to learn geometry
from masters. They seem to have been educated in classical geometry,
and I'm awed to see how they applied its harmonious patterns to
their designs. But analyzing photographic images of art can be
deceptive without knowing the object's actual dimensions. One
sign that a classical pattern is present is the existence
of a consistent theme. In this cabinet, the theme is the "square
root of two", the interplay of the square with the "root-two
rectangle" which emerges from it. While the numerical value
of the square root of two is approximately 1.4142... to 1, we
don't need to use numbers at all to understand it. We can see
it geometrically, and can replicate it using a compass and straightedge.
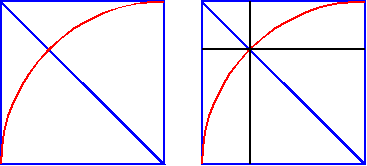
To understand the cabinet's whole design, we
start most simply, with a square. The diagonal of a square, which
is always 1.4142... times the length of the side of the square,
can help it to reach beyond itself to become a larger rectangle.
Simply put, the diagonal of a square becomes the side of a "root-two
rectangle" (i.e., for those who are numerically interested:
the long and short sides of this entire rectangle relate as 1.4142...
to 1. The size of every element of the cabinet's design can be
calculated from this single fact).
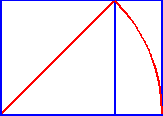
The act of swinging a compass between
the corners of the square, along the diagonal, to create the arc
is then repeated, creating "root-two rectangles" from
the square like fountains in three directions.
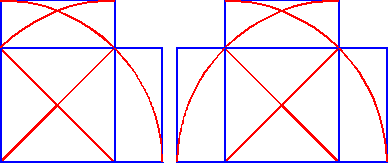
That's really enough to show us the
essential frame of the cabinet's geometric design.
Completing the geometric construction's
small, obviously missing squares at the upper corners
reveals the overall rectangle by which the cabinet appears to
have been designed.
(To it's friends and admirers, this rectangle is known numerically
as the "1.29288... rectangle" because that's the ratio
of its width to its height.)
Another interesting way to see this
same rectangle is to realize
that the arc made from one side of the square, centered at its
corner,
crosses the square's diagonal at a point which subdivides the
square
into two smaller "root-two rectangles" overlapping at
right angles within the square.
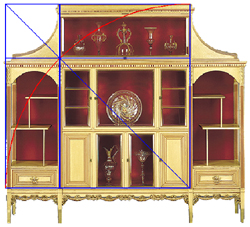
This construction shows us that the
cabinet's geometry can also be understood
as being formed by the overlapping of two such squares.
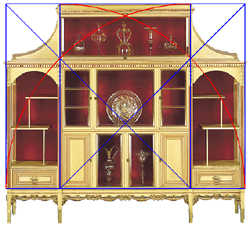
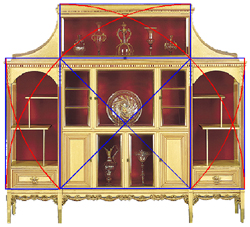
Within this overall frame, the guidelines
for the cabinet's details
can easily be discovered by continuing to apply the root-two theme.
Now we call upon two horizontal root-two rectangles overlapping
from the central square.
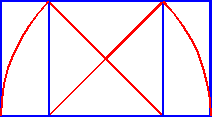
Repeating this in miniature within
the top of the design's central square
shows us the limits of the cabinet's central windows and frames
(below left).
Replicating this construction below itself
reveals the design of the lower central part of the cabinet (below
right).
But notice how it leads us below the overall rectangle
to show us the limit line of the ornamentation.
These are the subtle skills of a master designer
who knows how to weave necessary differences into sublime harmonies.
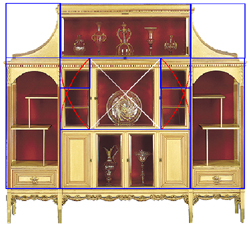
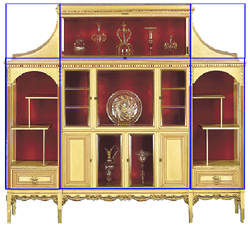
What about the details within the cabinet's
side panels?
We saw how the side panels came about as extensions from the original
central square
in the process of creating root-two rectangles.
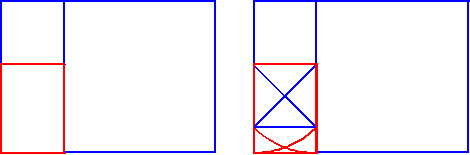
But now it's useful to know that a root-two rectangle's excess
section beyond the square
is itself a smaller square plus a root-two rectangle (below left).
This red rectangle is a smaller, turned model of the whole root-two
rectangle.
The important idea to a designer is that the part models the whole.
And this red root-two rectangle can
be considered, by definition, (below right)
to be made of a square whose (blue) diagonals swing the (red)
arcs.
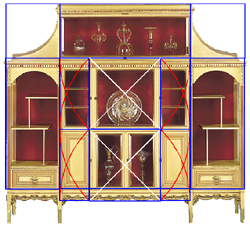
Applying this timeless truth to the
side panels of the cabinet at first shows us the dimensions of
the lower panel.
Now notice the shelves above the lower
panels.
They have been called asymmetrical due to their unusual stance.
But an understanding of geometry reveals that they are truly symmetric
in the classic sense.
While today "symmetry" often refers to a kind of mirror-image
equal reflection,
the Greek definition of "symmetry" was that parts and
whole shared "alike measure".
The parts are in accord with all other parts and with the whole
at once.
Wholeness and harmonious accord, traits of what is Good and True,
were once required for art, crafts and architecture to be considered
truly Beautiful
and healthy for the soul to gaze at.
Many philosophers of antiquity, and whole civilizations including
Egypt, China and India,
knew that exposing people, especially children, to harmony in
all its forms helps create harmonious people and societies.
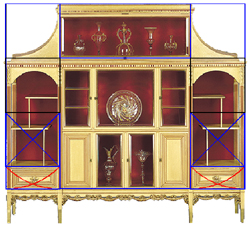
So, to see the symmetry of these shelves,
we must look to the eternally true idea we saw above
about the diagonal and arc of a square crossing to subdivide a
square into overlapping root-two rectangles.
When this construction is spun within
the lowest square of each of the cabinet's side sections,
in the root-two rectangle whose square generated the rectangle
of the lowest golden panels,
the curtain of unsymmetry is pulled away to reveal how the lower
shelf and its vertical support are integral
with the root-two theme which has cast a unified, benificent spell
over the entire design.
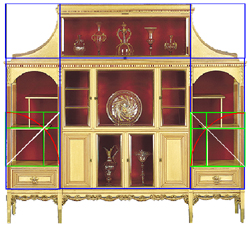
How are the cabinet's other shelves
determined? And the tapered legs?
I'll leave them for you to discover. There's usually more than
one way to find each.
But I assure you that you'll only need to know about squares,
and the "root-two rectangles" which sprout from their
diagonals.
Perhaps you'd like to construct from scratch the whole geometric
plan?
Start with a square and it's diagonal will show you where to go.
Perhaps you can explore and develop the symmetry further than
the great Herter Brothers did.
For its excellence, their work was, and remains, admired and very
expensive.
But you can explore for yourself the time-tested root-two theme
behind it,
whose true root is the eternal Truth of mathematics,
and for no charge at all.
Text and Images (c) 2003 Michael
S. Schneider
To see any of these geometric analyses, click
on its name:
The North Rose Window of Chartres Cathedral
The West Rose Window of the Cathedral Of St. John The
Divine (NY)
The East Rose
Window of Grace Cathedral (SF)
==================================
If you enjoy doing geometric constructions
or want to learn how,
consider these workbook companions to
"A Beginner's Guide To Constructing The Universe"
(Volume 4 specifically addresses
this Herter Cabinet and many related examples!)
Constructing The Universe Activity
Books
Create and Explore Geometric
Patterns
of Nature and Art
by
Michael S. Schneider
Ideal for Artists, Craftspeople, Architects, Designers,
Home Schools
and anyone who wishes to be inspired
by the relationships of mathematics with nature and human creativity.
Filled with hands-on geometric constructions and activities.
Many Illustrations. Easy To Understand. Self-Paced.
Available Only Through This Website!
Click here to learn about
these Activity Books
and see their Tables Of Contents.
==================================
Back to the Constructing
The Universe home page.